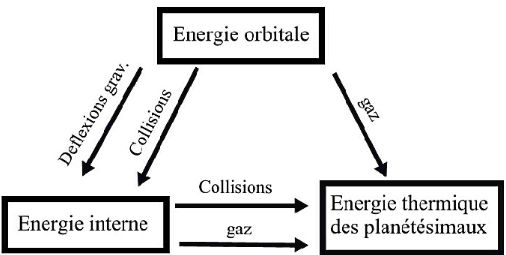
 |
|
|
Les déflexions gravitationnelles dues aux
rencontres mutuelles.
Ces rencontres convertissent de l'énergie associée
au mouvement orbital en mouvement aléatoire. En termes « hydrodynamiques
» les interactions gravitationnelles donnent une viscosité
au disque. Cette viscosité alimente le disque en énergie
interne (chaleur) grâce au cisaillement keplerien.
NOTE DE COURS : le cisaillement képlerien
Le "cisaillement képlérien" est la propriètè
qu'on les orbites d'avoir une vitesse orbitale variable avec la distance
au corps central. En termes plus clairs, cela signifie que la vitesse de
rotation varie avec la distance. Dans un disque képlérien
(les planètes par exemple), la vitesse orbitale est proportionnelle
à la puissance -1/2 de la distance au corps central. Ainsi, si l'on
considére deux corps initialement trés proches l'un de l'autre
et suivante des orbites circulaires de rayon légérement trés
différents, ils ne vont pas à la même vitesse. Au bout
d'un certain temps, ils finissent toujours par s'éloigner l'un de
l'autre.Cela s'oppose à la rotation "solide" qu'aurait un disque
de métal autour de son axe central : dans ce cas il n'y a pas de
"cisaillement" car dux points
initialement proches sur le disque solide resteront toujours
proches. Dans un disque képlérien, on tourne d'autant plus
vite que l'on est proche du centre.
C'est une propriété particulièrement
importante des disque képlérien car s'il y a cisaillement
il a inévitablement frottement. En effet, considérons
deux anneaux de matiere concentriques,et qui se touchent. Celui à
l'intérieur tourne plus vite que celui qui est à l'extérieur.
Sur la ligne de contacte entre les deux, des particules lentes (appartenant
à l'anneau externe) touchent et rentrent en collision avec des particules
rapides (appartenant à l'anneau interne). Ces rencontres et collisions
sont à l'origine d'une viscosité (qui n'est autre
qu'un transfert de quantité de mouvement), qui se traduit par un
transfert de chaleur. Par exemple quand je frotte une surface (mouvement
lent) avec du papier de verre (mouvement rapide) il se crée de la
chaleur. C'est plus ou moins le même phénoméne.
Les collisions physiques inélastiques.
Elles peuvent se traduire soit par une accrétion, soit par un rebond, soit par une fragmentation (catastrophique ou non). L'issue d'une collision est déterminée par la vitesse de rencontre, par la masse et par les propriétés mécaniques des corps en présence. A l'instar des déflexions gravitationnelles, les collisions convertissent de l'énergie associée au mouvement orbital en mouvements aléatoires (énergie interne du disque), mais avec une efficacité plus faible que les déflexions gravitationnelles (pour des rencontres « classiques » à faible vitesse). En effet, une partie de l'énergie associée aux mouvements aléatoires est transférée aux planétésimaux eux-mêmes, sous forme d'énergie thermique, qui sera ensuite rayonnée. Les collisions remplissent donc un double rôle de « réchauffement » et de « refroidissement » du disque. Prés de l'équilibre thermodynamique, c'est avant tout le mécanisme de «refroidissement » qui domine.
Le frottement avec le gaz
Le frottement des planétésimaux sur le
gaz (qui a une vitesse orbitale différente) se traduit par une dissipation
de l'énergie interne (refroidissement) ainsi qu'orbitale (modification
des orbites). Les rôles de ces différentes interactions sont
résumés dans la suivante.
 |
|
|
Le taux d'accrétion des corps est intimement
lié à leur vitesse relative (ou vitesse d'agitation) car
elle détermine la probabilité d'impact entre deux corps et
l'issue d'une rencontre. Il est donc de première importance d'en
avoir une estimation. L'interaction du gaz avec les planétésimaux
est la partie la plus simple du problème et peut être résolue
avec les équations de Gauss. Les corps dont la taille est inférieure
au kilomètre voient leur inclinaison et excentricité (inclinaison
et excentricité mesurent « l'écart » à
l'orbite circulaire) diminuer rapidement et donc favoriser
les rencontres à faible vitesse.
Cependant, l'effet des collisions et des déflexions
gravitationnelles est beaucoup plus difficile à estimer. La
manière la plus rigoureuse de traiter le problème est de
s'inspirer de la théorie cinétique des gaz, et de décrire
le système à l'aide de la fonction (f) de densité
dans l'espace des phases : f(x,v,t) dr dv est le nombre de corps à
l'instant t dans le volume d'espace des phases drdv centré sur le
point (r,v). Cette approche a été adoptée par de nombreux
auteurs (Goldreich et Tremaine 1978 ; Barge et Pelat 1990,1991 ; Hornung
et al. 1985). Le point de départ consiste à poser l'équation
de Boltzman (ou équation de Vlasov collisionnelle), en choisissant
un opérateur décrivant les collisions physiques et un autre
décrivant les déflexions gravitationnelles. L'équation
d'évolution de f prend la forme suivante (faussement simple)
:
| Equation 1 | 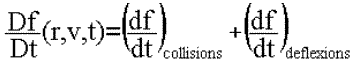 |
où D est la dérivée totale de f (incluant le potentiel). Le premier problème vient du choix des opérateurs de collisions et de déflexions qui peuvent être très complexes, en particulier dans le cas des rencontres gravitationnelles. L'équation 1. est ensuite multipliée successivement par 1, V, V^2,V^3, et puis moyennée en intégrant sur les vitesses. On obtient ainsi une série infinie d'équations qui décrivent l'évolution des différents moments de la fonction de distribution des vitesses f. Comme on ne peut traiter une hiérarchie infinie d'équations, une « relation de fermeture » est nécessaire pour ne prendre en compte qu'un nombre fini d'équations.
Cette approche, la plus généraliste, mène très rapidement à des calculs d'une grande complexité dont l'interprétation physique est particulièrement ardue. De plus, pour les besoins de la relation de fermeture, un certain nombre d'hypothèses doit être introduit (par exemple un faible libre parcours moyen). Celles-ci limitent finalement le champ d'application de cette approche. Pour simplifier cette dernière, une technique souvent utilisée à l'heure actuelle consiste à supposer que la vitesse moyenne locale est proche de la vitesse keplerienne circulaire et que les orbites sont toutes déphasées (ce qui est parfaitement raisonnable quand les perturbations gravitationnelles sont faibles). Dans ce cas, la seule variable indépendante est la vitesse d'agitation locale. Cette approche a été utilisée historiquement par Safronov, puis plus récemment par de nombreux auteurs (Wetherill et Stewart 1988, Ohtsuki 1999, Stewart et Ida 2000, à titre d'exemples). Pour les besoins de ce chapitre d'introduction, nous estimons la vitesse relative d'équilibre en nous basant sur une démonstration simplifiée (Greenberg 1982) mais qui garde l'essence des phénomènes en jeu.
Supposons que deux corps de même masse m se rencontrent
avec une vitesse relative v. Il nous faut calculer la variation de
magnitude de v, donnée par ![]() dans le cas de rencontres gravitationnelles et de rencontres collisionnelles.
Pour une rencontre gravitationnelle, nous nous plaçons dans l'hypothèse
(très approximative) où la déflexion peut être
modélisée par une diffusion à deux corps, du type
Rutherford :
dans le cas de rencontres gravitationnelles et de rencontres collisionnelles.
Pour une rencontre gravitationnelle, nous nous plaçons dans l'hypothèse
(très approximative) où la déflexion peut être
modélisée par une diffusion à deux corps, du type
Rutherford :
| Equation 2 | 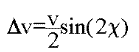 |
| Equation 3 | 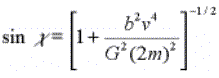 |
où v est la vitesse relative à l'infini, ![]() est
la magnitude de la variation de v (projetée sur un axe), b est le
paramètre d'impact, G est la constante de gravitation universelle.Pour
prendre en compte toutes les interactions de la particule avec le disque,
il faut sommer
est
la magnitude de la variation de v (projetée sur un axe), b est le
paramètre d'impact, G est la constante de gravitation universelle.Pour
prendre en compte toutes les interactions de la particule avec le disque,
il faut sommer ![]() sur tous les
paramètres d'impacts. De plus, le nombre de corps rencontrés
en un temps dt avec un paramètre d'impact db et une vitesse relative
v est :
sur tous les
paramètres d'impacts. De plus, le nombre de corps rencontrés
en un temps dt avec un paramètre d'impact db et une vitesse relative
v est :![]() , où s est la
densité surfacique de corps. Nous négligeons ici l'épaisseur
du disque devant son extension radiale, sur laquelle est intégré
b. On obtient une équation d'évolution de v^2:
, où s est la
densité surfacique de corps. Nous négligeons ici l'épaisseur
du disque devant son extension radiale, sur laquelle est intégré
b. On obtient une équation d'évolution de v^2:
| Equation 4 | 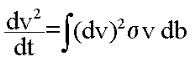 |
Nous nous plaçons donc dans le cas où v
est la seule vitesse différentielle keplerienne( cas où il
n'y a aucune agitation thermique et où seule demeure la roration
diférentielle). Entre deux points espacés de la distance
b, la vitesse relative v est approximativement b [dVk/dr] = n b/2 où
n est la fréquence orbitale et Vk est la vitesse orbitale keplerienne.
L'intégrale (Équation 4) donne alors :
| Equation 5 | 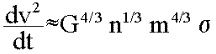 |
où sont omises les constantes multiplicatives,
qui ne modifient pas l'ordre de grandeur. Nous voyons dans l'équation
5 que le cisaillement keplerien produit de l'énergie interne à
un taux constant qui dépend uniquement de la masse des corps, de
la densité et de la vitesse orbitale locale. De leur côté,
les collisions dissipent une partie de l'énergie associée
aux mouvements aléatoires. Lors d'une collision la variation de
vitesse est (à un facteur près) égale à v.
Le facteur multiplicatif correspond au coefficient de restitution de la
collision. Il est en général de l'ordre de 50%. Le nombre
de collisions en un temps dt est donné par A ![]() v
/ h où h est l'épaisseur du disque, qui est de l'ordre de
v/n, A est la section efficace (~ pi r^2 , en supposant que les vitesses
relatives sont de l'ordre de la vitesse d'évasion). Le taux de perte
d'énergie due aux collisions est alors :
v
/ h où h est l'épaisseur du disque, qui est de l'ordre de
v/n, A est la section efficace (~ pi r^2 , en supposant que les vitesses
relatives sont de l'ordre de la vitesse d'évasion). Le taux de perte
d'énergie due aux collisions est alors :
| Equation 6 | 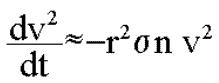 |
En écrivant l'équilibre énergétique,
on obtient une estimation de la vitesse d'équilibre (Greenberg 1982)
:
| Equation 7 | 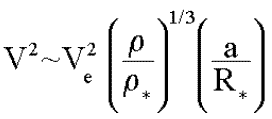 |
où ![]() et
et ![]() sont respectivement la
densité du corps et la densité du soleil, et où R*
est le rayon du soleil. Ce calcul très simplifié nous donne
à 1 unité astronomique :
sont respectivement la
densité du corps et la densité du soleil, et où R*
est le rayon du soleil. Ce calcul très simplifié nous donne
à 1 unité astronomique :
| Equation 8 |
Cette estimation est un peu forte, cependant elle nous indique que les vitesses relatives sont globalement de l'ordre de la vitesse d'évasion. En effet des calculs rigoureux et plus réalistes, comme ceux menés par Safronov (1969) , Wetherill et Stewart (1989), Barge et Pelat (1990) s'accordent sur ce point crucial :
Les vitesses relatives à l'équilibre dans un disque de planétésimaux sont de l'ordre de la vitesse d'évasion des corps dominants (~10 m/s).
Ce résultat très important est confirmé
par les simulations numériques (Aarseth et Palmer, 1993 par exemple).
Pour des vitesses d'évasion typiques de l'ordre de 10 m/s, les excentricités
et inclinaisons des planétésimaux sont de l'ordre de quelques
10^-4 (entre 1 et 3 unités astronomiques) ce qui est très
faible (environ quelques centièmes des excentricités des
planètes actuelles). Pour caractériser l'état d'excitation
du disque, on introduit donc naturellement un paramètre, ![]() ,
appelé " paramètre de Safronov " qui est une mesure du rapport
des vitesses relatives aux vitesses d'évasion des corps :
,
appelé " paramètre de Safronov " qui est une mesure du rapport
des vitesses relatives aux vitesses d'évasion des corps :
| Equation 9 | 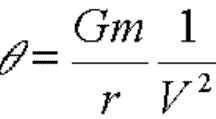 |
Comme nous allons le voir maintenant, la croissance des planétésimaux dépend de manière cruciale de ce paramètre.
| Equation 10 | 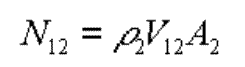 |
où A2 est la section efficace, ![]() et
V12 la vitesse relative des deux populations. En exprimant explicitement
A, l'équation 10 devient :
et
V12 la vitesse relative des deux populations. En exprimant explicitement
A, l'équation 10 devient :
| Equation 11 | 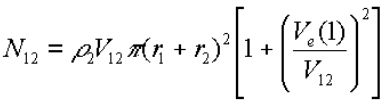 |
où r1 et r2 sont le rayon des particules 1 et 2 respectivement,
et où Ve(1) est la vitesse d'évasion de la particule 1. Nous
nous plaçons dans l'hypothèse simple où un gros corps
(de masse m1 et de rayon r1) accrète des corps beaucoup plus petits
(de masse m2 et de rayon r2) La densité spatiale de ces derniers
est ![]() . Nous faisons de plus
l'hypothèse d'accrétion parfaite, c'est à dire le
cas très optimiste où chaque rencontre se traduit par une
accrétion. Les taux d'accrétion s'écrivent de manière
générale :
. Nous faisons de plus
l'hypothèse d'accrétion parfaite, c'est à dire le
cas très optimiste où chaque rencontre se traduit par une
accrétion. Les taux d'accrétion s'écrivent de manière
générale :
| Equation 12. a | 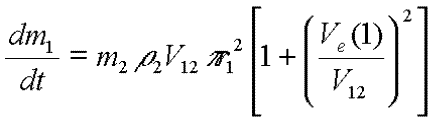 |
| Equation 12. b | 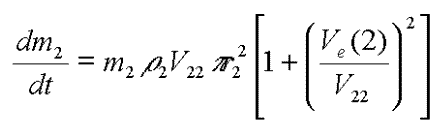 |
Le taux d'accroissement relatif des deux populations est donc donné
par :
| Equation 13 | 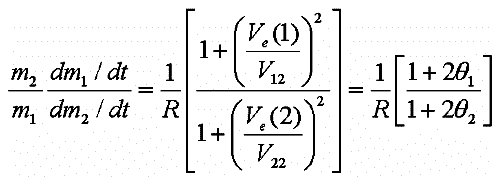 |
où R=r1/r2 >> 1; ![]() 1
et Les vitesses d'agitation dans le disque sont indirectement reliées
à q qui nous indique quels sont les corps dominants. Si q < 3
alors la majeure partie de la masse est dans les gros corps. Dans le cas
contraire, la masse est contenue dans les petits corps. De nombreuses simulations
numériques (Greenberg 1978, Weidenshilling et al. 1997 par exemple)
montrent que la masse du système demeure toujours dans les corps
de petite taille, correspondant à la population 2 dans notre modèle
simplifié. Il vient donc V << Ve(1) (où V est la vitesse
relative, et V12~V22). En conséquence q1 >> 1 et q2~1. En remarquant
de plus que q1=q2 x R2 (car q1 µ r12), l'Équation 13 se transforme
ainsi :2 et sont les paramètres de Safronov des deux populations
( ce qui est une entorse à la définition de ce paramètre,
car historiquement
1
et Les vitesses d'agitation dans le disque sont indirectement reliées
à q qui nous indique quels sont les corps dominants. Si q < 3
alors la majeure partie de la masse est dans les gros corps. Dans le cas
contraire, la masse est contenue dans les petits corps. De nombreuses simulations
numériques (Greenberg 1978, Weidenshilling et al. 1997 par exemple)
montrent que la masse du système demeure toujours dans les corps
de petite taille, correspondant à la population 2 dans notre modèle
simplifié. Il vient donc V << Ve(1) (où V est la vitesse
relative, et V12~V22). En conséquence q1 >> 1 et q2~1. En remarquant
de plus que q1=q2 x R2 (car q1 µ r12), l'Équation 13 se transforme
ainsi :2 et sont les paramètres de Safronov des deux populations
( ce qui est une entorse à la définition de ce paramètre,
car historiquement ![]() n'est défini
que par rapport aux gros corps). A partir de l' Équation 13 nous
pouvons distinguer deux régimes de croissance possibles. Si le terme
de droite est inférieur à 1, alors le taux de croissance
des deux populations tend asymptotiquement vers la même valeur, ce
qui correspond à une croissance ordonnée (décrite
par Safronov). Par contre, si le terme de droite est supérieur à
1, les corps grandissent d'autant plus rapidement qu'ils sont massifs,
ce qui est un mécanisme instable et aboutit à l'effet " Boule
de Neige ". Les vitesses relatives dans un disque de planétésimaux
sont de l'ordre de la vitesse d'évasion des particules qui sont
dynamiquement dominantes. La masse de ces dernières nous est donnée
par la distribution de taille, qui peut être en général
décrite par une loi de puissance :
n'est défini
que par rapport aux gros corps). A partir de l' Équation 13 nous
pouvons distinguer deux régimes de croissance possibles. Si le terme
de droite est inférieur à 1, alors le taux de croissance
des deux populations tend asymptotiquement vers la même valeur, ce
qui correspond à une croissance ordonnée (décrite
par Safronov). Par contre, si le terme de droite est supérieur à
1, les corps grandissent d'autant plus rapidement qu'ils sont massifs,
ce qui est un mécanisme instable et aboutit à l'effet " Boule
de Neige ". Les vitesses relatives dans un disque de planétésimaux
sont de l'ordre de la vitesse d'évasion des particules qui sont
dynamiquement dominantes. La masse de ces dernières nous est donnée
par la distribution de taille, qui peut être en général
décrite par une loi de puissance :
| Equation 14 | 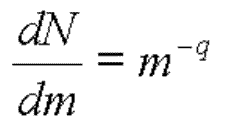 |
Les vitesses d'agitation dans le disque sont indirectement reliées
à q qui nous indique quels sont les corps dominants. Si q < 3
alors la majeure partie de la masse est dans les gros corps. Dans le cas
contraire, la masse est contenue dans les petits corps. De nombreuses simulations
numériques (Greenberg 1978, Weidenshilling et al. 1997 par exemple)
montrent que la masse du système demeure toujours dans les corps
de petite taille, correspondant à la population 2 dans notre modèle
simplifié. Il vient donc V << Ve(1) (où V est la vitesse
relative, et V12~V22). En conséquence ![]() 1
>> 1 et
1
>> 1 et ![]() 2~1. En remarquant
de plus que
2~1. En remarquant
de plus que ![]() 1=
1=![]() 2
x R^2 (car
2
x R^2 (car ![]() 1 proportionnel
à r1^2), l'Équation 13 se transforme ainsi :
1 proportionnel
à r1^2), l'Équation 13 se transforme ainsi :
| Equation 15 | 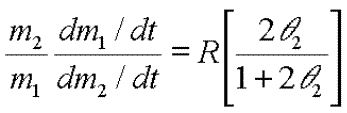 |
Le terme de droite dans l'Équation 15 est très supérieur à 1, donc le plus gros corps grossit de plus en plus rapidement par rapport aux plus petits. C'est la clef de l'effet "Boule de Neige". Ceci s'explique qualitativement d'une manière aisée : quand le plus gros corps n'impose pas sa dynamique au système (il ne contrôle pas les vitesses relatives), les vitesses de rencontres demeurent très inférieures à la vitesse de libération de ce dernier. Sa section efficace gravitationnelle est donc très grande. Il accrète donc très efficacement les petites particules de son environnement. En retour, sa masse augmente ainsi que sa section efficace. Le mécanisme s'emballe alors et le plus gros corps se " détache " progressivement de la distribution de masse : il devient l'unique représentant de la population la plus massive du système. Depuis, d'autres approches confirment également l'existence du mécanisme d'accrétion Boule de Neige (Spaute et al. 1991; Wetherill Stewart 1989, Stewart et Ida 1999, Kokubo et Ida 2000). Les temps caractéristiques de formation d'embryons planétaires à 1 u.a sont de l'ordre de quelques 10^4 à 10^5 ans (voir Figure 6) soit environ 1000 fois plus courts que dans le cas de " l'accrétion ordonnée " (premier modèle d'accrétion, décrit initialement en 1969 par Safronov). Une simulation numérique très récente (N-Corps) donne un temps de formation de 500 000 ans pour créer un corps de 10^26 g à 1 u.a (Kokubo et Ida, 2000). Wetherill et Setwart (1989) ont montré également que l'équipartition de l'énergie entre les populations de différentes masses joue un rôle déterminant pour le déclenchement de l'accrétion Boule de Neige. En effet, si un corps de masse m1 et de vecteur vitesse V1 rencontre un corps de masse m2 et de vitesse V2, on peut montrer simplement que le bilan de toute interaction sans perte d'énergie (ce qui est le cas d'une rencontre gravitationnelle) tend à équipartitionner l'énergie cinétique totale entre les deux corps, de sorte que M1 V1^2 = M2 V2 ^2 ( prodiot de la masse par le carre de la vitesse). Ainsi, les vitesses d'agitation des plus gros corps diminuent et les plus petits corps sont accélérés. Ce mécanisme d'équipartition s'appelle également "friction dynamique". En conséquence, les rencontres impliquant les plus gros corps se feront à une vitesse beaucoup plus faible que les rencontres entre petits corps, ce qui accroît d'autant le rapport des sections efficaces, et donc le taux de collisions. Encore une fois, les plus gros corps sont favorisés, et les plus petits sont ralentis dans leur croissance. Ohtsuki et Ida (1990) confirment indépendamment que l'accrétion Boule de Neige est favorisée si la vitesse d'agitation est une fonction décroissante de la masse, ce qu'implique la friction dynamique.
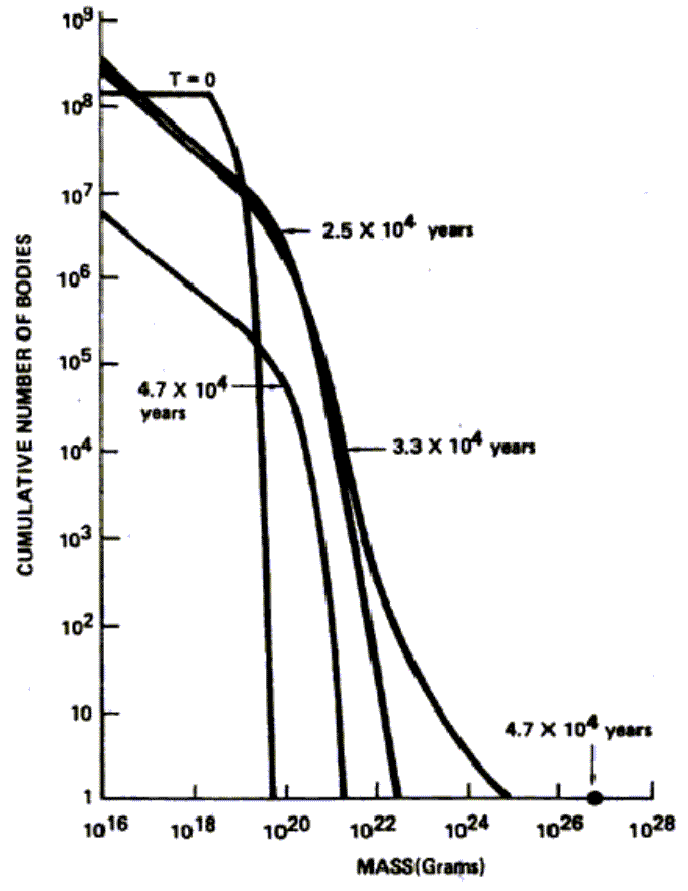
Evolution de la distribution de taille au cours de l'accrétion des planétésimaux à l'aide d'une simulation statistique. On voit clairement qu'en quelques 10^4 ans un embryon massif se sépare de la distribution de taille. (Wetherill et Stewart 1989)